Part 1:
Consider a right triangle with a=12 and c=13. What is the length of b?
Part 2:
Consider the following two groups of shapes:
4 right triangles with legs of 12 and x
1 square with side length x
1 square with side length 12
4 right triangles with legs of 12 and x
1 square with side length 13
Using the two groups, can you create two squares?
Do these squares have equal areas?
Why does this show that x^2+12^2=13^2?
Assignment:
Make comments below about the steps or methods you went through in each of Part 1 and 2. What methods did you consider using to answer the questions? What difficulties did you have? Think about if you had to present to the class, how would you explain to a classmate how you found the length of b without the use of Part 2, but rather coming up with your own method of showing how you found b. Also, consider the methods or difficulties of your classmates and respond if you had a similar experience to theirs, if you can help them, or if you had an experience very different from theirs.
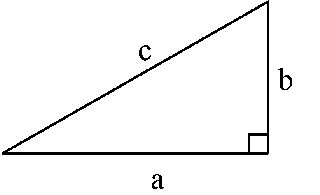
Finding the length of b was really easy, because I just plugged in a and c into the Pythagorean Theorem. However, when we were asked to how to show how we found b, I was at first a bit confused. I thought about using the cosine and sine functions with the right angle to possibly show the length of b, but I am not sure this would work.
ReplyDeleteI thought about somehow extending the length of each side into a square and then manipulating the squares to show that 12^2+x^2=12^2. I thought this was a good idea to create a square because then you could compare the area of the two smaller squares to the area of the larger square. This is similar to what was done in Part 2.